
This post outlines some of the technical issues and solutions connected with the development of Permutation Racer, the third game produced for my PhD research.
Permutation Racer is an experimental, endless racing game, exploring the procedural construction of space.
It’s part of an ongoing investigation of ideas that connect games, permutation and the sublime. The race track is generated from a series of noise filtered ‘biome’ styling functions. There are about 12 region types ranging from chasms to archways and caves, all generated in real time as the player progresses. The objective is simply to travel as far as possible. More generalised information about the game and a download of the software is available at this link. A description of the approach developed for Permutation Racer is outlined below.
Endless Voxel Track
Permutation Racer uses Voxel Isosurfaces to produce its endless tracks. This technique is based on the marching cubes algorithm, a process which transforms a 3d array of density points into a polygonised mesh. There is some good documentation of this technique available here. In short these polygonising algorithms take an array of density values, like a point cloud and traverse the array in voxels, marking the points where the density values shift from interior to exterior values. The difference between ‘inside’ and ‘outside’ is defined as a threshold value, usually between 0 and 1 (though this can be -1 to +1 depending on the density values used). The threshold value dictates the point in a density spectrum where the voxel ‘skin’ lies. For example, if the threshold value was .1 the following string of numbers would be skinned as a small hill-like curve .2 .3 .4 .5 .4 .3 .2. If the threshold was raised to .6 nothing would be polgonised as all the density values are under the threshold. You can see the effect of changing the density threshold in the webplayer here. A solidity threshold of 0 will lead to ‘fuller’ forms whereas a higher values result in a more sparse voxel space. Since Permutation Racer uses a mathematical noise field (simplex) to provide the underlying density values, increasing the frequency of the noise function will also effect the size and number of voxelised ‘blobs’ polygonised in a chunk. The image below demonstrates the sort of effects these parameters can have (density threshold on the y-axis and frequency of noise on the x-axis).

The resolution of the voxel grid is entirely down to the requirements of the game, but a more detailed resolution and larger volume will obviously take longer to calculate. The process of voxelisation is therefore best seperated into individual chunks, so that the game world can be defined/polygonised/rendered/culled on threads. In Permutation Racer each chunk of world consists of a cubic volume containing x=22,z=22,y=16 voxels. The resolution of the resulting mesh can be seen in the chunks below.
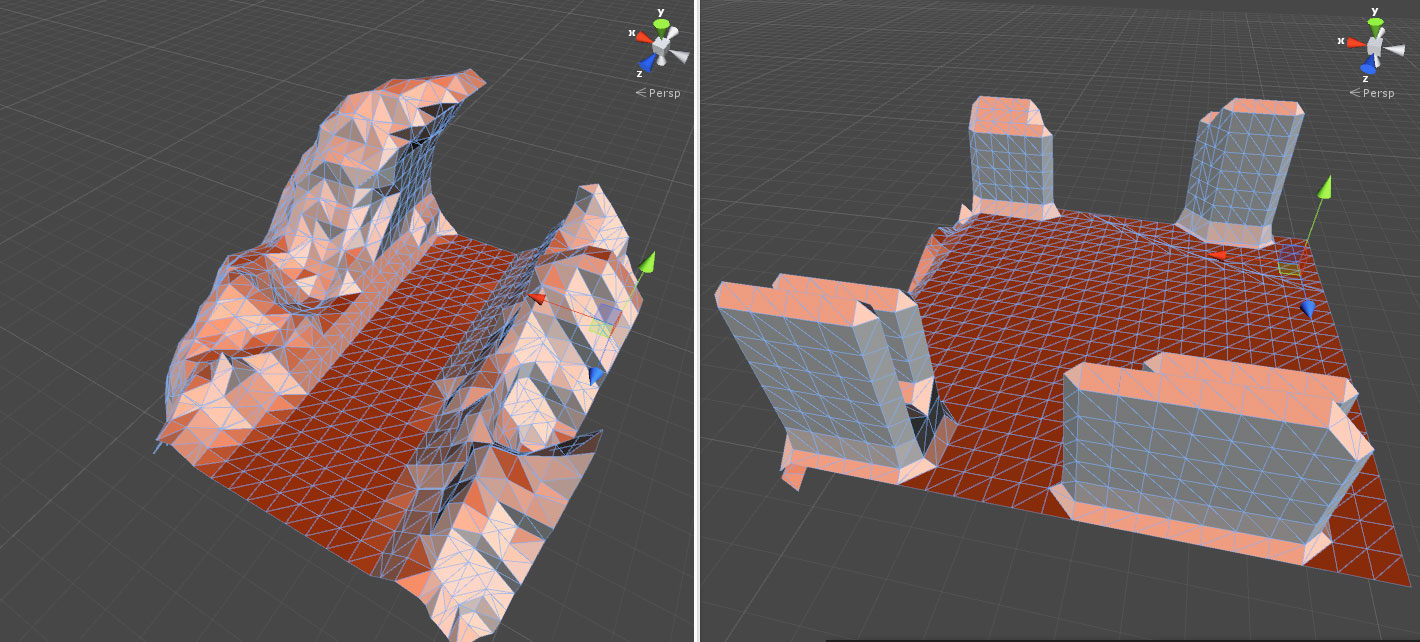
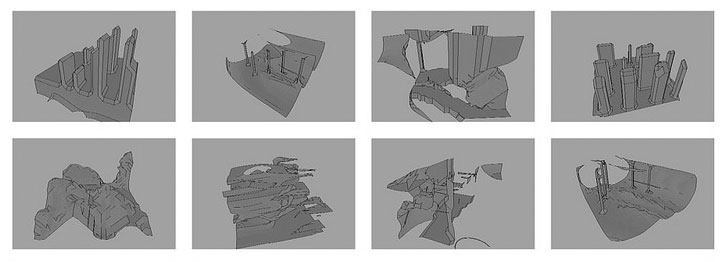
These chunks are processed in threads and positioned in the game scene in a linear path to build the racetrack. The image below demonstrates a range of individual chunks, produced from different underlying point cloud data.
In the actual game the adjacent chunks that make up the racertrack polygonise adjoining areas of the density array so that chunks remain continuous and readable.
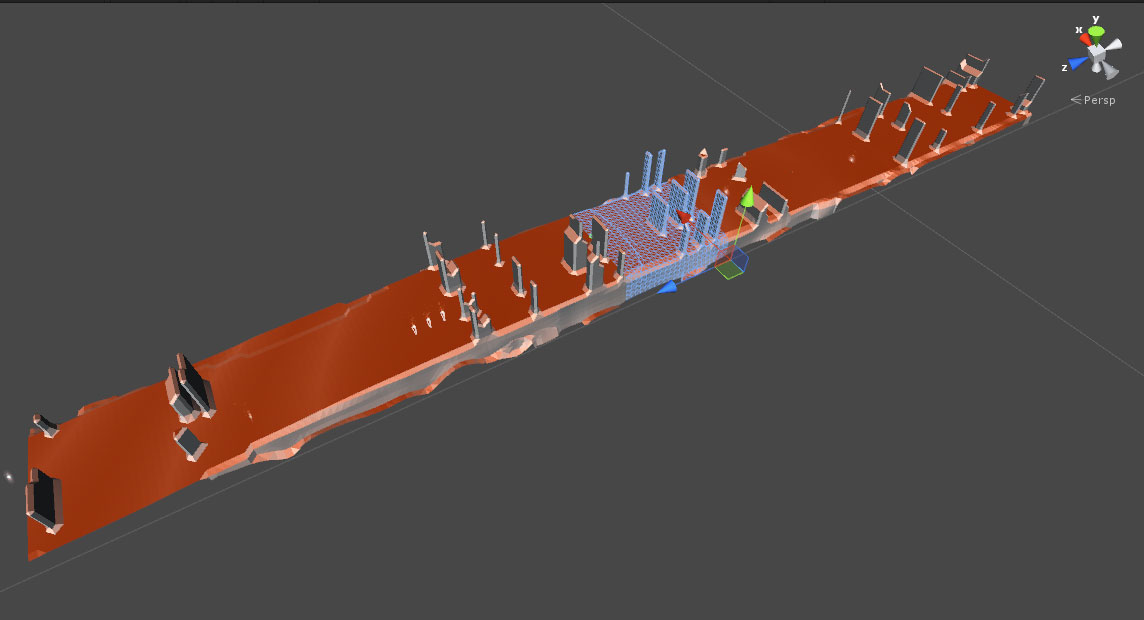
The image below shows a long section of track, click here to open the image and zoom in to see the details
Noise to Signal
As with all procedural generation the key to making the resulting world interesting is making the underlying structure interesting. The image of voxel cubes earlier in this post demonstrates the sort of features a simple noise field can create. However, the results are very chaotic and don’t feel organic or purposeful. Players generally enjoy exploring worlds that appear to have either history and purpose, and seem to have been created though geological processes or human intervention. Permutation Racer uses a series of synthesis approaches to generate interesting underlying data forms. These synthesis techniques are primarily based on the layering and filtering of fractal noise. In fact the term synthesis neatly references the approach of musical synthesizers which use similar techniques to layer waveforms into richer and more interesting sound forms. This process is illustrated below (courtesy of http://www.planetoftunes.com/,https://documentation.apple.com/en/logicpro/)
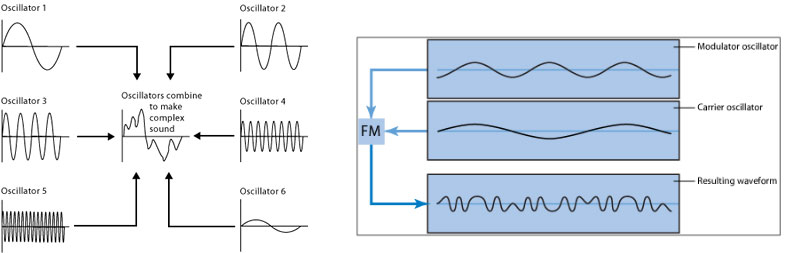
There are many types of synthesis, additive (shown above left) , subtractive and FM (frequency modulation,shown above right). Permutation Racer uses all of these techniques, but applies them to the output of noise functions rather than waveforms. Noise functions (simplex/perlin etc don’t have periodic cycles, but can be smoothed and produced at varying frequencies). The way these functions are layered gives the resulting forms specific characteristics. In Permutation Racer noise layers are modulated by each other and by other mathematical processes such as sinewaves and rounding functions. The image below demonstrates how the main track uses a combined sinewave function to produce the curves in the racetrack. The distortion or ‘curviness’ of the track is increased along the x axis, where the x-value in world space is used to multiply a secondary waveform that distorts the original sinewave (see the FM example above).

This function is calculated for every x,y,z point requested by the polygonising algorithm. Instead for returning unmodified noise, the program returns a noisefield that is modified by many attributes, all of which are based on the spatial location of the request. For example, the GetNoise(x,y,z) function will return 1 for all points that are outside the current sine centre plus a margin amount. This causes the track to follow the sinewave curve and have cliff-walls at its sides. The width of the track is then controllable with the margin variable, which itself can be linked to x distance and other noise function. The GetNoise() function might also introduce increasing amounts of random noise as the y-axis rises over a specific ceiling. This will cause spikes and undulations to form a ceiling over the track. Its the development and combination of these filters that allows the engine to produce interesting geometry.
Permutation Racer contains a library of GetNoise() functions that produce different terrain; forests, tunnels, corridors, causeways. In fact the game simultaneously calculates two types at all times and interpolates the results before passing the final value back to the polgonising algorithm. This allows the gameworld to blend between different terrain forms as the player progresses. The image below (from an early prototype) shows a forest generation function (left) mixed with a cave generation function (Right).

It only takes a few modifications to use the techniques discussed above for generating a wide range of different game worlds, even spherical ones!

